B2b signal of Chinese positioning satellite BeiDou Part 1

Introduction

China’s BeiDou third generation satellite (BDS-3) is broadcasting a new positioning signal, PPP-B2b (precise point positioning-B2b signal). I will try decoding this PPP-B2b signal.

B2b signal

The BDS-3 series satellites consist of three orbital satellites: medium earth orbit (MEO), inclied geosynchronous orbit (IGSO), and geostationary orbit (GEO).

From the Positioning satellite list compiled on the QZSS official page, the PRN (psuedo random noise) numbers of the BDS-3 series satellites are:

1. MEO: C19 C20 C21 C22 C23 C24 C25 C26 C27 C28 C29 C30 C32 C33 C34 C35
2. IGSO: C36 C37 C41 C42 C43 C44 C45 C46 C38 C39 C40
3. GEO: C59 C60 C61

The B2b signal of interest here is broadcast from the BDS-3 series satellite in BPSK(10) with a frequency of 1207.14 MHz, a bandwidth of 20.46 MHz, and a symbol rate of 1 ksym/s. From the B2b signal of BDS-3, new navigation message B-CNAV3 is transmitted in MEO and IGSO. On the other hand, the single precision positioning message PPP-B2b is broadcast as B2b signal in GEO. Of the receivers I have, Pocket SDR and Septentrio mosaic-X5 can receive this B2b signal. Settings changed from the initial values In the mosaic-X5 receiver, C59 and C60, which broadcast PPP-B2b messages, was confirmed.

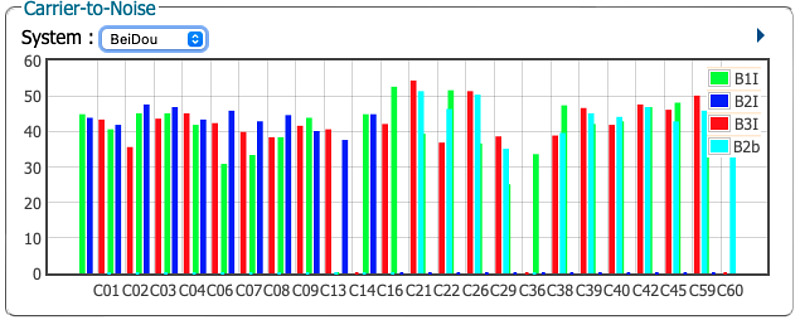
A B2b signal sample for mosaic-X5 receiver is available at QZS L6 Tool. From that top directory, we can check the receiver raw data BDSRawB2b of the B2b signal as follows:

python/septread.py -c < sample/20230819-081730hasbds.sept | lv

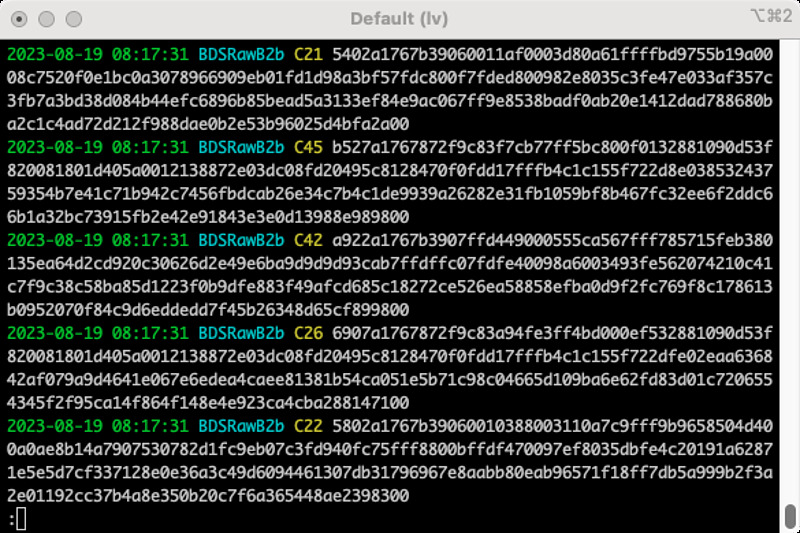
The format is common between B-CNAV3 and PPP-B2b. Message contents are distinguished by a 6-bit message type (Mestype). Message type numbers 10, 30, and 40 are used as B-CNAV3. Additionally, message type numbers 1, 2, 3, 4, 5, 6, 7, and 63 are used for PPP-B2b.

In both cases, the message length is 1,000 symbols. Therefore, one message is transmitted per second. The message carries a 16-symbol preamble (used to detect the beginning of the message), a 6-symbol PRN, and a 972-symbol body, including the Mestype. An error correction code based on iterative decoding called a low density parity check (LDPC) code is applied to this text.

Error correction requires the transmission of redundant information. This transmission includes block codes, in which message and parity are clearly separated in the codeword, and convolutional codes, in which codewords are created according to a fixed rule from past messages. LDPC codes are classified as block codes, and it may be possible to extract messages without LDPC decoding.

Iterative decoding is a method based on the idea of increasing the effectiveness of error correction by randomizing the residual errors after error correction. Turbo codes and LDPC codes are famous as such codes, but LDPC codes are often used for bits of 1000 or more, and turbo codes are often used for bits less than 1000 bits. LDPC codes are also used in high-speed Ethernet and other applications because they can divide received words and process them in parallel.

LDPC check matrix

However, B2b signals use a multilevel LDPC code that collects information bits into 6-bit units and performs error correction. Many LDPC codes are binary, ans handling this B2b signal requires effort.

This parity check matrix is specified in section 6.1.3 of the specification BDS-SIS-ICD-PPP-B2b-1.0. This matrix is huge, consisting of 81 rows and 162 columns. However, many of the elements are zero, and when looking at the 162 column elements in any one row, there are only 4 elements that have values. Therefore, in the specifications, this check matrix H is expressed by the matrix H_index of the location indicating non-zero and its element value H_element. Figure 6.2 has a flowchart for creating H from this H_index and H_element, but it is difficult to understand.

Based on this flowchart, I created a code to calculate the parity check matrix. Because it’s just a matrix slice, any language that can handle two-dimensional matrices will work. Here, I wrote it in Rust. I created a directory with cargo new bds-b2b, wrote the following code in the automatically created src/main.rs, and executed it with cargo run.

fn main() {
    let h_i = [
        [ 19, 67, 109, 130 ],
        ..
        [  9, 51,  90, 132 ],
    ];
    let h_e = [
        [ 46, 45, 44, 15 ],
        ..
        [ 22, 15, 12, 33 ],
    ];
    let mut h = [[0; 162]; 81];
    for i in 0..81 {
        for j in 0..4 {
            let row = i;
            let col = h_i[i][j];
            h[row][col] = h_e[i][j];
        }
    }
    for row in 0..81 {
        println!("{:?},", h[row]);
    }
}

The code that does not omit the matrix part and its execution result are posted on github. A huge queue will appear by clicking this.

Decoding 64-ary LDPC code

The next thing I should do is read, understand, and code the Non-binary LDPC encoding and decoding method in the Annex of the specification. Section 1 has encoding and decoding examples. I will need to type this into your PC for verification.

Section 2 describes two methods for this non-binary LDPC decoding. The first method, the extended min-sum method, is a common method in binary LDPC decoding that calculates message passing to check nodes by calculating the logarithmic likelihood ratio (LLR). Because this article describes the method using 64-ary operations, it is calculated on Galois field.

The second method, the fixed path decoding method, which I feel is the recommended method by this author, uses something called a fixed path deviation value vector. However, I couldn’t think of a specific calculation method because it involves complex exclusive OR calculations and long set calculations that change depending on specific conditions.

Broadly speaking, methods for changing the error correction ability by the estimated number of erroneous symbols, such as Weldon’s difference-set cyclic codes (1966). It may be discretizing LLR that takes continuous values.

But why did it use 64-value LDPC code? I think that multileveling shortens the code length, and there is no benefit in terms of error correction performance or efficiency. I would like to think about what the motivation is.

While I’m looking for a paper on this fixed path decoding method and reading it, I’m thinking of writing a decoder and reading B2b messages by taking advantage of the characteristic of block codes, where the information bits appear as they are. We still have a long way to go.

Related article(s):

• B2b signal of Chinese positioning satellite BeiDou Part 2 8^th April 2024
• BeiDou B2b signal livestream 13^th November 2023