Creating a positioning satellite skyplot using Python
Introduction
To know one’s coordinates using only radio waves from positioning satellites, positioning signals from at least four satellites are required. This is because four variables at the user’s position are unknown: latitude, longitude, ellipsoid height, and time.
It is preferable to be able to observe as many satellites as possible for positioning. I created a Python code that displays the positions of such positioning satellites in the sky.
Skyplot
For example, the satellite position display app [GNSS View] (https://qzss.go.jp/technical/gnssview/index.html) released by the Cabinet Office, Government of Japan, allows you to see the visible positions of positioning satellites at any location and any time. This is a screenshot of the position of the European Galileo satellites that will be observable in Hiroshima on November 23, 2023 at 23:20:00 UTC (November 24, 08:20:00 Japan time), plotted in GNSS View.
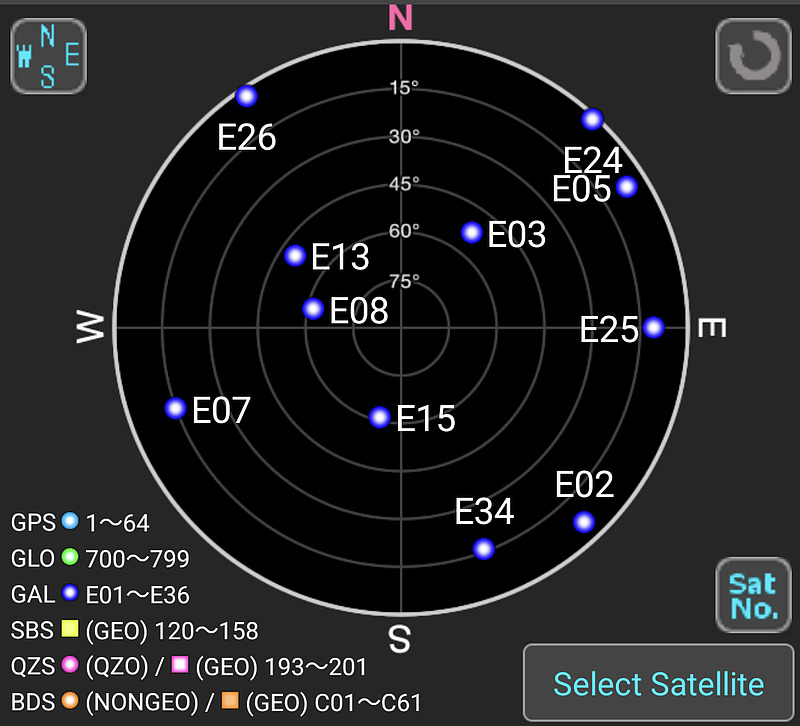
This diagram shows the direction and elevation angle at which positioning satellites can be seen from your own position, and is called a skyplot.
The open source GNSS-Radar, released by Professor Taro Suzuki of Chiba Institute of Technology, can display the positions of positioning satellites in a browser without an Internet connection. I use GNSS-Radar to find out the locations of positioning satellites.
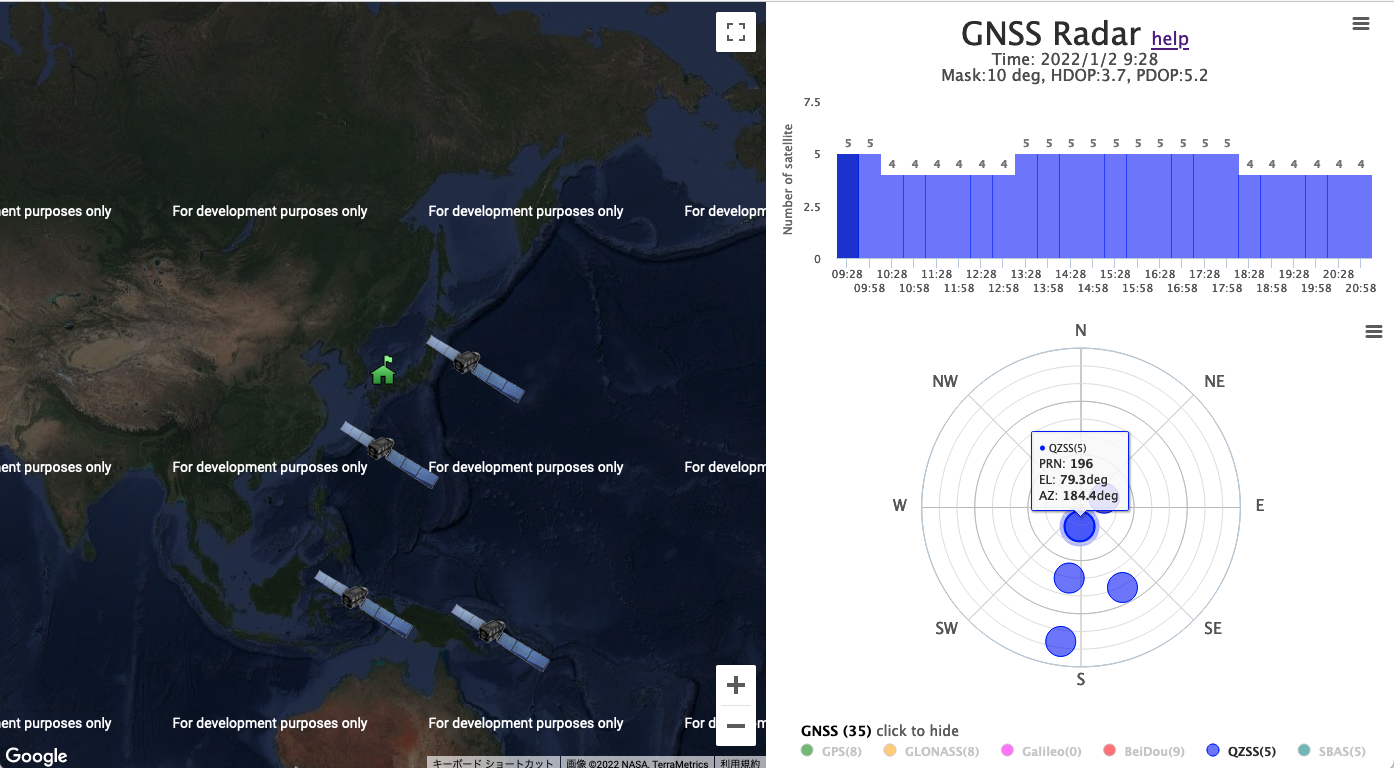
As you can see, there are several ways to know the locations of positioning satellites.
On the other hand, grayscale images in PDF format are preferable for creating reports, and you would like to create your own skyplots to highlight specific satellites and show observation conditions on the diagram. Also, to load such diagrams into, say LaTeX, a PDF file containing images in vector format is preferable, rather than a bitmap file such as a PNG or JPG file.
In order to create a skyplot with your own code, you will need to obtain the satellite orbits.
Two line element
Satellite positioning requires ephemeris, which shows the exact orbit of the satellite. On the other hand, to display a sky plot, it is sufficient to know the approximate satellite position, and for this purpose, two line elements (TLE) are often used. This is a two-line text format that shows the orbital inclination angle and other information required to represent the satellite orbit.
Such TLEs can be obtained from CelesTrak. Strictly speaking, satellite orbits may change from moment to moment, but unless orbital corrections are being made, the TLE is not expected to change significantly. The lifespan of an ephemeris is two hours, but once downloaded, the TLE can be used for a while. For example, the TLE of the recently launched Advanced Radar Satellite Daichi-4 is expressed as follows:
ALOS-4 (DAICHI-4)
1 60182U 24123A 24229.54940804 .00000500 00000+0 73855-4 0 9998
2 60182 97.9215 325.3457 0001395 98.1122 28.2230 14.79473854 6861
Here, we will try to obtain the TLEs of all European Galileo satellites from CelesTrak.
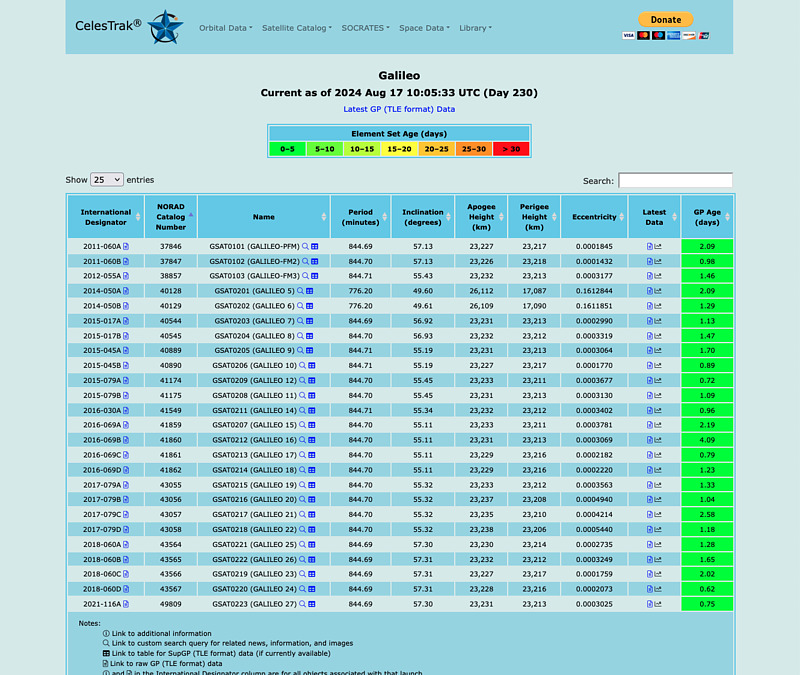
Click the document icon in the Latest Data column to display the TLE in your browser, then copy and paste it into a text file. Repeat this process for all Galileo satellites.
Skyplot creation using Python
Next, based on the TLE, we calculate the direction and elevation of the satellite from an arbitrary coordinate point. For coordinate calculation and display, we used Python’s non-standard modules skyfield, numpy, and matplotlib.
pip install skyfield numpy matplotlib
The code will display available satellites in the dictionary satellites1 with a circle, while unavailable satellites in satellites2 will be displayed with a cross. In addition, unavailable satellite numbers will be grayed out. In this example, the available satellites are E03, E07, E08, E13, and E15. E stands for Europe, which is a Galileo satellite. The order of the TLEs is arbitrary. The observation point is Hiroshima (coordinates 34.23N, 132.27E), and the date and time are 23:30:00 UTC on November 22, 2023.
skyplot.py
#! /usr/bin/env python
# -*- coding: utf-8 -*-
FILENAME = 'skyplot'
FONTSIZE = 16
# GAL TLE can be obtained from:
# https://celestrak.org/norad/elements/table.php?GROUP=galileo&FORMAT=tle
from skyfield.api import Topos, load, wgs84
from skyfield.sgp4lib import EarthSatellite
import numpy as np
from matplotlib import pyplot as plt
import datetime
# TLE data
satellites1 = {
"E03": ["1 41860U 16069B 24075.03714384 .00000000 00000+0 00000+0 0 9997",
"2 41860 55.0417 123.9214 0003428 309.7138 50.3288 1.70474893 45607"],
"E07": ["1 41859U 16069A 24075.76931632 -.00000003 00000+0 00000+0 0 9996",
"2 41859 55.0449 123.9045 0005163 290.7537 69.2607 1.70474715 45362"],
"E08": ["1 41175U 15079B 24077.45505889 -.00000001 00000+0 00000+0 0 9994",
"2 41175 55.3797 123.8317 0004223 301.5343 58.4922 1.70474689 51340"],
"E13": ["1 43567U 18060D 24073.22747821 -.00000102 00000+0 00000+0 0 9991",
"2 43567 57.3051 4.0560 0004572 309.8424 50.1177 1.70475162 35092"],
"E15": ["1 43564U 18060A 24073.15310948 -.00000102 00000+0 00000+0 0 9996",
"2 43564 57.3028 4.0542 0005044 303.0742 56.8777 1.70475060 35093"],
}
satellites2 = {
"E11": ["1 37846U 11060A 24070.59038482 -.00000094 00000+0 00000+0 0 9990",
"2 37846 57.1269 4.2009 0004048 0.9151 359.0813 1.70475681 76996"],
"E12": ["1 37847U 11060B 24075.36853573 -.00000108 00000+0 00000+0 0 9993",
"2 37847 57.1277 4.0716 0005128 340.5417 117.7805 1.70475226 77083"],
"E19": ["1 38857U 12055A 24077.08212499 -.00000003 00000+0 00000+0 0 9991",
"2 38857 55.3621 124.1355 0005270 267.6966 92.3107 1.70473587 70991"],
"E20": ["1 38858U 12055B 24075.29159274 -.00000001 00000+0 00000+0 0 9992",
"2 38858 55.3626 124.1864 0002996 263.1608 96.8769 1.70473746 70965"],
"E18": ["1 40128U 14050A 24076.38068143 -.00000063 00000+0 00000+0 0 9995",
"2 40128 49.7505 306.7902 1607231 147.6212 223.3476 1.85519539 63054"],
"E14": ["1 40129U 14050B 24077.17831918 -.00000057 00000+0 00000+0 0 9995",
"2 40129 49.7668 305.8335 1605771 148.4561 222.2616 1.85520304 65236"],
"E26": ["1 40544U 15017A 24073.30254099 -.00000102 00000+0 00000+0 0 9991",
"2 40544 56.9222 4.0745 0004144 291.6220 68.3342 1.70475448 55129"],
"E22": ["1 40545U 15017B 24074.14320105 -.00000105 00000+0 00000+0 0 9990",
"2 40545 56.9283 4.0665 0003375 281.1733 78.7899 1.70475327 18189"],
"E24": ["1 40889U 15045A 24076.84456596 .00000028 00000+0 00000+0 0 9998",
"2 40889 55.2656 244.3185 0005887 44.3383 315.6720 1.70473651 52993"],
"E30": ["1 40890U 15045B 24075.30543699 .00000030 00000+0 00000+0 0 9994",
"2 40890 55.2642 244.3563 0003840 46.2777 313.7129 1.70473690 52990"],
"E09": ["1 41174U 15079A 24077.23534912 -.00000002 00000+0 00000+0 0 9999",
"2 41174 55.3811 123.8397 0004688 303.6832 56.3397 1.70474783 50768"],
"E02": ["1 41549U 16030A 24076.99092123 .00000028 00000+0 00000+0 0 9995",
"2 41549 55.4130 244.3111 0003383 18.6658 341.3102 1.70473716 48653"],
"E01": ["1 41550U 16030B 24076.10899448 .00000030 00000+0 00000+0 0 9998",
"2 41550 55.4111 244.3364 0001211 357.6320 2.3289 1.70473751 48631"],
"E04": ["1 41861U 16069C 24077.75112543 -.00000001 00000+0 00000+0 0 9990",
"2 41861 55.0457 123.8527 0005491 274.6415 85.3637 1.70473447 45518"],
"E05": ["1 41862U 16069D 24074.96434658 .00000001 00000+0 00000+0 0 9994",
"2 41862 55.0430 123.9236 0004700 275.5406 84.4789 1.70474973 45591"],
"E21": ["1 43055U 17079A 24076.04030420 .00000030 00000+0 00000+0 0 9994",
"2 43055 55.3883 244.1605 0000736 22.1381 337.8261 1.70474387 38952"],
"E25": ["1 43056U 17079B 24076.91865947 .00000028 00000+0 00000+0 0 9998",
"2 43056 55.3883 244.1362 0001720 316.3645 43.5851 1.70474520 38986"],
"E27": ["1 43057U 17079C 24073.03300014 .00000027 00000+0 00000+0 0 9997",
"2 43057 55.3924 244.2419 0002160 350.7256 9.2233 1.70474360 38903"],
"E31": ["1 43058U 17079D 24076.77253818 .00000029 00000+0 00000+0 0 9993",
"2 43058 55.3864 244.1366 0001974 300.9948 58.9487 1.70474451 38996"],
"E33": ["1 43565U 18060B 24075.13123991 -.00000108 00000+0 00000+0 0 9993",
"2 43565 57.3054 4.0028 0003358 282.1792 77.7846 1.70475082 35161"],
"E36": ["1 43566U 18060C 24073.59351374 -.00000103 00000+0 00000+0 0 9995",
"2 43566 57.3052 4.0464 0004542 314.0609 45.9024 1.70475319 35115"],
"E34": ["1 49809U 21116A 24074.42529437 -.00000106 00000+0 00000+0 0 9990",
"2 49809 57.2961 3.9185 0001376 281.4869 183.9787 1.70475239 14122"],
"E10": ["1 49810U 21116B 24075.39474642 -.00000108 00000+0 00000+0 0 9998",
"2 49810 57.2968 3.8907 0001282 308.3744 144.5609 1.70475412 14162"],
}
# Load timescale and observer position
ts = load.timescale()
t = ts.utc(2023, 11, 22, 23, 30, 0)
observer = Topos(latitude_degrees=34.23, longitude_degrees=132.27)
# Initialize satellite objects
satellite_objects1 = {sat: EarthSatellite(satellites1[sat][0], satellites1[sat][1], sat, ts) for sat in satellites1}
satellite_objects2 = {sat: EarthSatellite(satellites2[sat][0], satellites2[sat][1], sat, ts) for sat in satellites2}
# Plotting
fig, ax = plt.subplots(subplot_kw={'projection': 'polar'},
figsize=(6, 6))
ax.set_theta_zero_location('N')
ax.set_theta_direction(-1)
ax.set_ylim(0, 90) # Altitude 0° (horizon) to 90° (zenith)
for sat in satellite_objects1:
difference = satellite_objects1[sat] - observer
topocentric = difference.at(t)
alt, az, distance = topocentric.altaz()
if alt.degrees > 0: # Only plot if above the horizon
r = 90 - alt.degrees
theta = np.radians(az.degrees)
ax.plot(theta, r, 'o', c='black')
ax.text(theta, r, f'{sat}', fontsize=FONTSIZE, ha='right', va='bottom')
for sat in satellite_objects2:
difference = satellite_objects2[sat] - observer
topocentric = difference.at(t)
alt, az, distance = topocentric.altaz()
if alt.degrees > 0: # Only plot if above the horizon
r = 90 - alt.degrees
theta = np.radians(az.degrees)
ax.plot(theta, r, 'x', c='gray')
ax.text(theta, r, f'{sat}', fontsize=FONTSIZE, ha='right', va='bottom', c='gray')
ax.set_rmax(90)
ax.set_rticks([0, 30, 60, 90]) # Altitude rings
ax.set_rlabel_position(-22.5) # Move radial labels
ax.set_rgrids([0, 30, 60, 90], labels=["90", "60", "30", "0"], fontsize=FONTSIZE)
ax.grid(True)
ax.set_thetalim([0, 2*np.pi])
ax.set_thetagrids(np.rad2deg(np.linspace(0, 2*np.pi, 5)[1:]),
labels=["E", "S", "W", "N"], fontsize=FONTSIZE)
plt.savefig(FILENAME + '.pdf')
#plt.savefig(FILENAME + '.svg')
#plt.savefig(FILENAME + '.tiff', dpi=600)
#plt.savefig(FILENAME + '.jpg', dpi=600)
#plt.savefig(FILENAME + '.png', transparent=True, dpi=600)
plt.show()
When you run this code with ./skyplot.py, the sky plot will be displayed on the screen and a PDF file of it will be output. By modifying the source code, you can change the output format to SVG, TIFF, JPG, or PNG, change the observation point or observation time continuously, or display various additional information.
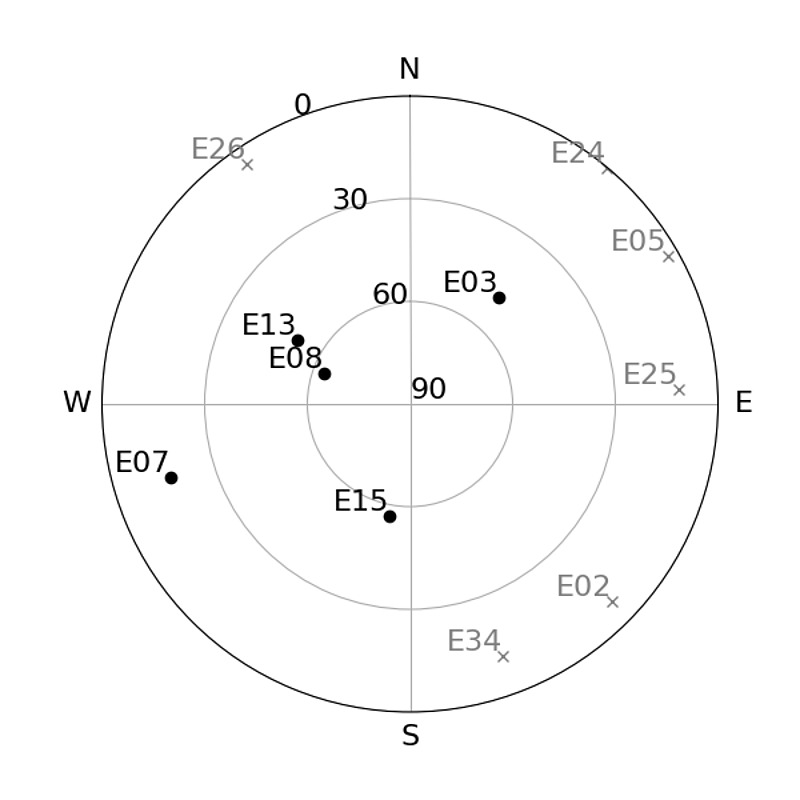
Conclusion
I got the 2-line orbital elements TLE from CelesTrak and created a sky plot with my own Python code. With such a code at hand, you can create a sky plot of any satellite at any point, which is useful for various verifications.